Lost Pieces - Locietta's Blog

Appearance

游戏王MD中的概率问题（二）：Bo2与升降段 ​

前言 ​

不能输的理由
不能输的理由

如前文所说，一次11连后手引起了我计算MD相关概率问题的兴趣。在完成了n连硬币正面概率的计算后，本篇文章将讨论已知卡组胜率的情况下升降段机制对对局数量的要求，以及特殊赛制的公平性问题。

文中涉及到马尔科夫链和鞅论的一些知识，可以查阅这篇文章来了解。其中关于一维随机游走问题的计算也有助于理解本文中的计算。

TL;DR ​

这篇文章的主要计算结果都在这里，如果你对冗长的计算没什么兴趣也许可以不看之后的计算。结果就已经挺冗长了

实卡无穷对局连胜K局问题 ​

AB双方无限对局，由A首先先攻，单局胜者下一局后攻。当某一方首先获得单局KK连胜时视为游戏胜利。第一局（主卡局），卡组A对卡组B的先攻胜率为p0p_0；在备牌局，卡组A的先攻胜率为p1p_1，后攻胜率为p2p_2。

分出胜负所需局数的期望EE由以下方程组给出

{E1=(E−1+11−p2)(1−p2K−1)E−1=(E1+1p1)(1−(1−p1)K−1)E=(1−p0)E−1+p0E1+1\begin{dcases} E_1=\left(E_{-1}+\dfrac{1}{1-p_2}\right)\left(1-p_2^{K-1}\right) \\ E_{-1}=\left(E_{1}+\dfrac{1}{p_1}\right)\left(1-(1-p_1)^{K-1}\right)\\ E=(1-p_0)E_{-1}+p_0E_1+1 \end{dcases}

A获得最终游戏胜利的概率是

p+=p2K−1[1−(1−p0)(1−p1)K−1](1−p1)K−1+p2K−1−(1−p1)K−1p2K−1p^+=\dfrac{p_2^{K-1}\left[1-(1-p_0)(1-p_1)^{K-1}\right]}{(1-p_1)^{K-1}+p_2^{K-1}-(1-p_1)^{K-1}p_2^{K-1}}

特别地，当K=2K=2时，

E=2+p0+p1p2−p0(p1+p2)1−p1+p1p2p+=p2(p0+p1−p0p1)1−p1+p1p2\begin{gather*} E=\dfrac{2+p_0+p_1p_2-p_0(p_1+p_2)}{1-p_1+p_1p_2}\\ p^+=\dfrac{p_2(p_0+p_1-p_0p_1)}{1-p_1+p_1p_2} \end{gather*}

如果双方使用完全相同的卡组（含side），那么p1+p2=1p_1+p_2=1；如果双方在MD打，没有side，那么p0=p1p_0=p_1。

MD天梯升降段问题 ​

设某卡组单局游戏胜率为p=p先+p后2p=\dfrac{p_{\text{先}}+p_{\text{后}}}{2}，假设刚升上某一小段，问升段/降段发生的期望局数，以及升段的概率。

钻石段/白金段 ​

累计4胜升段，0胜场3连败掉段。

E=2p5−4p4−p3+10p2−6p+3p6−5p5+11p4−13p3+11p2−5p+1p+=p4(p2−3p+3)p6−5p5+11p4−13p3+11p2−5p+1\begin{gather*} E=\dfrac{2p^5-4p^4-p^3+10p^2-6p+3}{p^6-5p^5+11p^4-13p^3+11p^2-5p+1}\\ p^+=\dfrac{p^4(p^2-3p+3)}{p^6 - 5 p^5 + 11 p^4 - 13 p^3 + 11 p^2 - 5 p + 1} \end{gather*}

大师段 ​

累计5胜升段，0胜场3连败掉段。

E=3p6−9p5+12p4−11p3+16p2−9p+32p6−10p5+22p4−24p3+16p2−6p+1p+=p5(p2−3p+3)2p6−10p5+22p4−24p3+16p2−6p+1\begin{gather*} E=\dfrac{3p^6 - 9p^5 + 12p^4 - 11p^3 + 16p^2 - 9p + 3}{2p^6 - 10p^5 + 22p^4 - 24p^3 + 16p^2 - 6p + 1}\\ p^+=\dfrac{p^5(p^2 - 3p + 3)}{2p^6 - 10p^5 + 22p^4 - 24p^3 + 16p^2 - 6p + 1} \end{gather*}

p=0.5p=0.5时，钻石段升段概率为63.6%63.6\%，大师段升段概率为58.3%58.3\%。单局胜率低于50%50\%的卡组升段的概率可以大于50%50\%。钻石段升降段期望局数约为13，大师段升降段期望局数约为10。

一般情况 ​

一般地，如果某小段需要累计NN胜升段，0胜场MM连败掉段，卡组单局胜率为pp。那么，能成功升段的概率为：

p+=−f(−M)f(N)−f(−M)p^+=\dfrac{-f(-M)}{f(N)-f(-M)}

其中，

f(n)={p2p−1[1−(1−pp)n],n≥01−(1−p)n,n<0f(n)=\begin{dcases} \dfrac{p}{2p-1}\left[1-\left(\dfrac{1-p}{p}\right)^n\right] &,n\geq 0\\ 1-(1-p)^n &,n<0 \end{dcases}

而升降段发生所需的期望局数EE由以下线性方程组给出：

{E1=N−12p−1+(E0−N2p−1)pN(1−p)−p(1−p)NpN+1−p(1−p)NE=(E1+1p)[1−(1−p)M]\begin{dcases} E_1=\dfrac{N-1}{2p-1}+\left(E_0-\dfrac{N}{2p-1}\right)\dfrac{p^N(1-p)-p(1-p)^N}{p^{N+1}-p(1-p)^N}\\ E=\left(E_1+\dfrac{1}{p}\right)\left[1-(1-p)^M\right] \end{dcases}

Bo∞中的连胜 ​

Bo3决定胜负的卡牌游戏

游戏王实卡的赛制是Bo3，也就是三局两胜制。在前一局游戏结束后，败方可以选择下一局的先后手，同时双方可以根据对方的卡组以及先后手情况从自己预先准备的15张备牌中更换一些针对卡。

由于换备和三局两胜制的存在，因此会比MD的一把定胜负更平衡一些。

Bo2赛制 ​

设想这样一种Bo2赛制： 双方无限对局，当某一方首先获得单局2连胜时视为游戏胜利。 理论上来说，相比Bo3赛制，这样会要求更大的玩家水平和卡组构筑差距才能决出胜负。

假设对局双方分别使用卡组A和卡组B，在第一局（主卡局），卡组A对卡组B的先攻胜率为p0p_0；在备牌局，卡组A的先攻胜率为p1p_1，后攻胜率为p2p_2.

为了简单起见，我们假设双方卡组都是先手比后手更有优势的卡组（没有玩天杯龙的）。因此当某个玩家输了一局的时候，下一局他一定会选择先手。

那么问题是，如果使用卡组A的玩家先攻：

  • 游戏期望在第几局结束？
  • 他的最终胜率是多少？

对局次数期望 ​

这个对局过程显然是马尔可夫的。对局总共有5种状态，S={−2,−1,0,1,2}S=\{-2, -1, 0, 1, 2\}，其中00是第一局（初始态），−2-2和22分别代表连输/连赢2次的状态（吸收态）。

我们可以写出相应的转移矩阵：

P=[100001−p100p1001−p00p0001−p200p200001]\mathcal{P}=\begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 1 - p_1 & 0 & 0 & p_1 & 0 \\ 0 & 1-p_0 & 0 & p_0 & 0 \\ 0 & 1-p_2 & 0 & 0 & p_2 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}

设从状态ii转移到某个吸收态的期望为EiE_i，则

{E−2=0E−1=(1−p1)E−2+p1E1+1E0=(1−p0)E−1+p0E1+1E1=(1−p2)E−1+p2E2+1E2=0\begin{cases} E_{-2}=0\\ E_{-1}=(1-p_1)E_{-2}+p_1E_1+1\\ E_0=(1-p_0)E_{-1}+p_0E_1+1\\ E_1=(1-p_2)E_{-1}+p_2E_2+1\\ E_2=0 \end{cases}

解得

{E−1=1+p11−p1+p1p2,E0=2+p0+p1p2−p0(p1+p2)1−p1+p1p2,E1=2−p21−p1+p1p2\begin{dcases} E_{-1} = \dfrac{1+p_1}{1-p_1+p_1p_2}, &\\ E_0 = \dfrac{2+p_0+p_1p_2-p_0(p_1+p_2)}{1-p_1+p_1p_2}, &\\ E_1 = \dfrac{2-p_2}{1-p_1+p_1p_2} \end{dcases}

也就是说，分出胜负的期望局数是E=E0=2+p0+p1p2−p0(p1+p2)1−p1+p1p2E=E_0=\dfrac{2+p_0+p_1p_2-p_0(p_1+p_2)}{1-p_1+p_1p_2}

获胜概率 ​

设对局中前一把赢了之后最终取胜的概率为AA，前一把输了之后最终取胜的概率为BB，利用

{A=p2+(1−p2)BB=p1A\begin{cases} A=p_2+(1-p_2)B\\ B=p_1A \end{cases}

解得(A,B)=(p21−p1+p1p2,p1p21−p1+p1p2)(A, B) = \left(\dfrac{p_2}{1-p_1+p_1p_2},\dfrac{p_1p_2}{1-p_1+p_1p_2}\right)

最终胜率为P=p0A+(1−p0)B=p2(p0+p1−p0p1)1−p1+p1p2P = p_0A+(1-p_0)B = \dfrac{p_2(p_0+p_1-p_0p_1)}{1-p_1+p_1p_2}

K连胜的情形 ​

之前我们讨论的是2连胜的情形，假如将胜利条件改为有一方KK连胜才结束那又如何计算呢？

获胜概率 ​

我们使用鞅与停时定理来计算一般情况下的概率。参考前文，为了计算概率，我们需要构造鞅f(Xn)f(X_n)，由定理4可知f(i)f(i)需要满足：

{f(i)=p2f(i+1)+(1−p2)f(−1),i>0f(i)=p1f(1)+(1−p1)f(i−1),i<0\begin{dcases} f(i)=p_2f(i+1)+(1-p_2)f(-1),& i>0 \\ f(i)=p_1f(1)+(1-p_1)f(i-1), & i <0 \end{dcases}

由初值无关性，我们不妨设f(0)=p0f(1)+(1−p0)f(−1)=0f(0)=p_0f(1)+(1-p_0)f(-1)=0，求解函数方程组（提示：当成共享边界条件f(0)=0f(0)=0的两个线性递推数列），不难得到，

f(n)={p2−n+1−p0,n>00,n=0−(1−p1)n+1+1−p0,n<0f(n)=\begin{dcases} p_2^{-n+1}-p_0 &,n>0\\ 0 &,n=0\\ -(1-p_1)^{n+1}+1-p_0 &,n<0 \end{dcases}

容易验证f(n)f(n)是有界的，所以我们可以使用停时定理，得到

0=f(0)=E(f(X0))=E(f(XT))=p+f(K)+(1−p+)f(−K)0 = f(0) = \mathbb{E}(f(X_0)) = \mathbb{E}(f(X_T)) = p^+f(K)+(1-p^+)f(-K)

因此

p+=−f(−K)f(K)−f(−K)=(1−p1)−K+1−1+p0p2−K+1−p0+(1−p1)−K+1−1+p0=p2K−1[1−(1−p0)(1−p1)K−1](1−p1)K−1+p2K−1−(1−p1)K−1p2K−1\begin{aligned} p^+&=\dfrac{-f(-K)}{f(K)-f(-K)}\\ &=\dfrac{(1-p_1)^{-K+1}-1+p_0}{p_2^{-K+1}-p_0+(1-p_1)^{-K+1}-1+p_0}\\ &=\boxed{\dfrac{p_2^{K-1}\left[1-(1-p_0)(1-p_1)^{K-1}\right]}{(1-p_1)^{K-1}+p_2^{K-1}-(1-p_1)^{K-1}p_2^{K-1}}} \end{aligned}

游戏局数的期望 ​

期望的计算还是一样，根据状态转移矩阵可以列出2K+12K+1元的线性方程组：

{Ei=(1−p2)E−1+p2Ei+1+1,i∈{1,⋯ ,K−1}Ei=p1E1+(1−p1)Ei−1+1,i∈{−1,⋯ ,−K+1}E0=(1−p0)E−1+p0E1+1EK=E−K=0\begin{dcases} E_i=(1-p_2)E_{-1}+p_2E_{i+1}+1 &,i\in \{1,\cdots,K-1\}\\ E_i=p_1E_1+(1-p_1)E_{i-1}+1 &,i \in \{-1, \cdots, -K+1\}\\ E_0=(1-p_0)E_{-1}+p_0E_1+1\\ E_K=E_{-K}=0 \end{dcases}

由于我们只关心E0E_0，简单化简后可以得到（提示：把前两行看成数列递推式）

{E1=(E−1+11−p2)(1−p2K−1)E−1=(E1+1p1)(1−(1−p1)K−1)E0=(1−p0)E−1+p0E1+1\begin{dcases} E_1=\left(E_{-1}+\dfrac{1}{1-p_2}\right)\left(1-p_2^{K-1}\right) \\ E_{-1}=\left(E_{1}+\dfrac{1}{p_1}\right)\left(1-(1-p_1)^{K-1}\right)\\ E_0=(1-p_0)E_{-1}+p_0E_1+1 \end{dcases}

具体的解就不写了，太长了😵

天梯升降段 ​

另一个有趣的问题是已知卡组的胜率为pp，如何计算在MD天梯升段/降段的期望局数和概率？

你可以考虑先攻胜率p1p_1后攻胜率p2p_2，但无非就是把每步转移概率里的pp换成(p1+p2)/2(p_1+p_2)/2

MD的段位机制如下：

  • 累计净胜KK局升段（白金/钻石段K=4K=4，大师段K=5K=5）
  • 净胜0局的情况下连败3局掉段
  • 掉段流程中只要有赢一局，回到净胜1局的状态

这个问题的解法和之前的KK连胜问题基本一样：

  • 根据状态转移矩阵列出线性方程组求解期望
  • 构造鞅使用停时定理来计算最终概率

读者可以参考上一节的计算，这里就简单写写。

钻石段：K=4K=4 ​

状态转移矩阵：

Mp=[100000001−p000p00001−p00p000001−p0p0000001−p0p0000001−p0p0000001−p0p00000001]\mathcal{M_p}=\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1-p & 0 & 0 & 0 & p & 0 & 0 & 0\\ 0 & 1-p & 0 & 0 & p & 0 & 0 & 0\\ 0 & 0 & 1-p & 0 & p & 0 & 0 & 0\\ 0 & 0 & 0 & 1-p & 0 & p & 0 & 0\\ 0 & 0 & 0 & 0 & 1-p & 0 & p & 0\\ 0 & 0 & 0 & 0 & 0 & 1-p & 0 & p\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix}

记E=(E−3E−2E−1E0E1E2E3E4)\mathbf{E}=\begin{pmatrix} E_{-3}\\ E_{-2}\\ E_{-1}\\ E_{0}\\ E_{1}\\ E_{2}\\ E_{3}\\ E_{4} \end{pmatrix}，c=(01111110)\mathbf{c}=\begin{pmatrix} 0\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 0 \end{pmatrix}，A=(2I62)\mathbf{A}=\begin{pmatrix} 2& &\\ & \mathbf{I}_{6} &\\ & & 2 \end{pmatrix}

解线性方程(A−Mp)E=c(\mathbf{A}-\mathcal{M_p})\mathbf{E}=\mathbf{c}，得

E=1p6−5p5+11p4−13p3+11p2−5p+1(02p3+2p2−p+1−2p4+2p3+5p2−3p+22p5−4p4−p3+10p2−6p+3−p5+5p4−11p3+15p2−9p+4p5−2p4−3p3+13p2−12p+5−2p5+12p4−29p3+36p2−22p+60)\mathbf{E}=\dfrac{1}{p^6-5p^5+11p^4-13p^3+11p^2-5p+1}\begin{pmatrix} 0\\ 2p^3+2p^2-p+1 \\ -2p^4+2p^3+5p^2-3p+2 \\ 2p^5-4p^4-p^3+10p^2-6p+3 \\ -p^5+5p^4-11p^3+15p^2-9p+4 \\ p^5-2p^4-3p^3+13p^2-12p+5 \\ -2p^5+12p^4-29p^3+36p^2-22p+6 \\ 0 \end{pmatrix}

为了计算升段概率，我们构造f(n)f(n)使{f(Xn)}\{f(X_n)\}是个鞅，

f(n)={p2p−1[1−(1−pp)n],n≥01−(1−p)n,n<0f(n)=\begin{dcases} \dfrac{p}{2p-1}\left[1-\left(\dfrac{1-p}{p}\right)^n\right] &,n\geq 0\\ 1-(1-p)^n &,n<0 \end{dcases}

停时T={首次到达n=4∨n=−3}T=\{ \text{\small 首次到达} n=4 \vee n=-3 \}，设升段概率为p+p^+，则由停时定理

f(0)=E(f(XT))=p+f(4)+(1−p+)f(−3)=0f(0)=\mathbb{E}(f(X_T))=p^+f(4)+(1-p^+)f(-3)=0

解得，

p+=−f(−3)f(4)−f(−3)=p4(p2−3p+3)p6−5p5+11p4−13p3+11p2−5p+1p^+=\dfrac{-f(-3)}{f(4)-f(-3)}=\dfrac{p^4(p^2-3p+3)}{p^6 - 5 p^5 + 11 p^4 - 13 p^3 + 11 p^2 - 5 p + 1}

大师段：K=5K=5 ​

状态转移矩阵：

Mp=[1000000001−p000p000001−p00p0000001−p0p00000001−p0p00000001−p0p00000001−p0p00000001−p0p000000001]\mathcal{M_p}=\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1-p & 0 & 0 & 0 & p & 0 & 0 & 0& 0\\ 0 & 1-p & 0 & 0 & p & 0 & 0 & 0& 0\\ 0 & 0 & 1-p & 0 & p & 0 & 0 & 0& 0\\ 0 & 0 & 0 & 1-p & 0 & p & 0 & 0& 0\\ 0 & 0 & 0 & 0 & 1-p & 0 & p & 0& 0\\ 0 & 0 & 0 & 0 & 0 & 1-p & 0 & p& 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1-p & 0 & p\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0& 1 \end{bmatrix}

解线性方程(A−Mp)E=c(\mathbf{A}-\mathcal{M_p})\mathbf{E}=\mathbf{c}，得

E=(03p4+3p2−2p+13p5−6p4+3p3−8p2+5p−23p6−9p5+12p4−11p3+16p2−9p+3−2p5+10p4−19p3+24p2−13p+43p6−14p5+29p4−35p3+32p2−17p+5−p5+8p4−22p3+32p2−21p+63p6−19p5+52p4−78p3+69p2−33p+70)2p6−10p5+22p4−24p3+16p2−6p+1\mathbf{E}=\dfrac{\begin{pmatrix} 0\\ 3p^4 + 3p^2 - 2p + 1\\ 3p^5 - 6p^4 + 3p^3 - 8p^2 + 5p - 2\\ 3p^6 - 9p^5 + 12p^4 - 11p^3 + 16p^2 - 9p + 3\\ -2p^5 + 10p^4 - 19p^3 + 24p^2 - 13p + 4\\ 3p^6 - 14p^5 + 29p^4 - 35p^3 + 32p^2 - 17p + 5\\ -p^5 + 8p^4 - 22p^3 + 32p^2 - 21p + 6\\ 3p^6 - 19p^5 + 52p^4 - 78p^3 + 69p^2 - 33p + 7\\ 0 \end{pmatrix}}{2p^6 - 10p^5 + 22p^4 - 24p^3 + 16p^2 - 6p + 1}

鞅和之前的一样（因为段位机制没变，只是停止条件变了），停时变成T={首次到达n=5∨n=−3}T=\{ \text{\small 首次到达} n=5 \vee n=-3 \}，此时

p+=−f(−3)f(5)−f(−3)=(p2−3p+3)p52p6−10p5+22p4−24p3+16p2−6p+1p^+=\dfrac{-f(-3)}{f(5)-f(-3)}=\dfrac{(p^2 - 3p + 3)p^5}{2p^6 - 10p^5 + 22p^4 - 24p^3 + 16p^2 - 6p + 1}

简单分析 ​

胜率 ​

我们把K=4K=4和K=5K=5时的胜率-升段率曲线画出来：

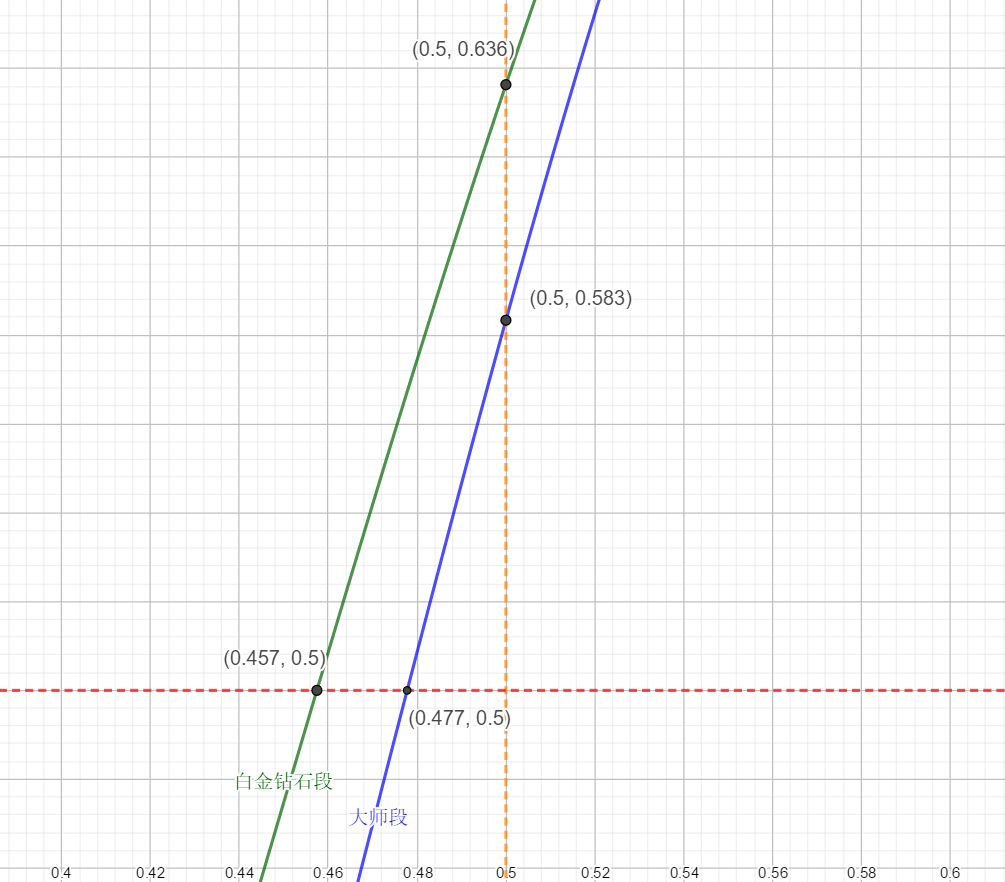胜率-升段率曲线
胜率-升段率曲线
  • 一个卡组要在天梯上保持不升不降，其胜率并不需要达到50%50\%：在白金/钻石段只需要46%46\%的胜率，而在大师段则需要48%48\%
  • 一个单局胜率在50%50\%的卡组实际上有60%60\%左右的概率是能升段的

游戏局数 ​

把K=4K=4和K=5K=5时的胜率-期望局数曲线画出来：

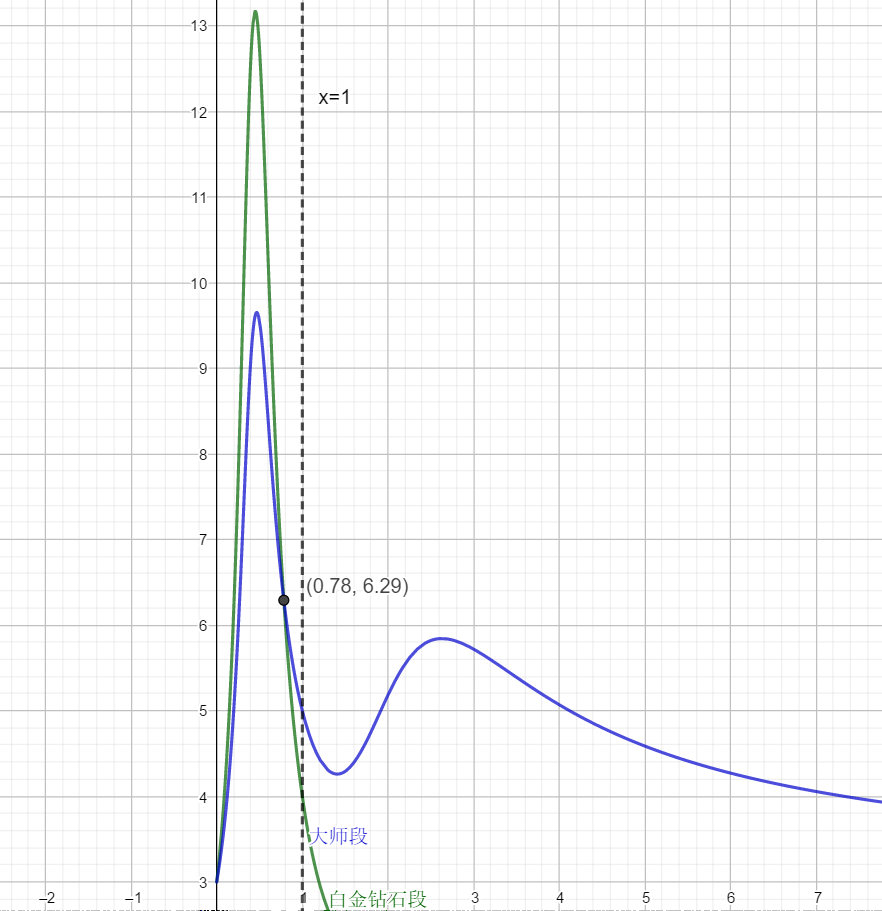胜率-期望局数曲线
胜率-期望局数曲线
  • 除非单局胜率特别高（>78%>78\%），不然大师段升降段会比钻石段更快（大概是因为掉段更容易？）
  • 期望局数在略小于50%50\%胜率的地方取到最大（不过并不是总体胜率50%50\%的点，还要更小一点）
  • 期望上来说，大师段10把升降段，钻石白金13把升降段

一般情况 ​

总结一下计算结果，如果某小段需要累计NN胜升段，0胜场MM连败掉段，卡组单局胜率为pp。

升段率 ​

由于段位机制没有变化，因此对应的鞅{f(Xn)}\{f(X_n)\}也不变：

f(Xn)={p2p−1[1−(1−pp)Xn],Xn≥01−(1−p)Xn,Xn<0f(X_n)=\begin{dcases} \dfrac{p}{2p-1}\left[1-\left(\dfrac{1-p}{p}\right)^{X_n}\right] &,X_n\geq 0\\ 1-(1-p)^{X_n} &,X_n<0 \end{dcases}

于是能成功升段的概率就是：

p+=−f(−M)f(N)−f(−M)p^+=\dfrac{-f(-M)}{f(N)-f(-M)}

期望 ​

升降段发生所需的期望局数由线性方程(A−Mp)E=c(\mathbf{A}-\mathcal{M}_p)\mathbf{E}=\mathbf{c}给出。其中，

A=(2IN+M−12),c=(01N+M−10),Mp=[1qpqp⋱⋮qpqp⋱⋱qpqp1], q=1−p\begin{gather*} \mathbf{A}=\begin{pmatrix} 2& &\\ & \mathbf{I}_{N+M-1} &\\ & & 2 \end{pmatrix},\mathbf{c}=\begin{pmatrix} 0\\ \mathbf{1}_{N+M-1}\\ 0 \end{pmatrix},\\ \mathcal{M}_p=\begin{bmatrix} 1 & & & & & & & & & \\ q & & & & & p & & & & \\ & q & & & & p & & & & \\ & & \ddots & & & \vdots & & & & \\ & & & q & & p & & & & \\ & & & & q & & p & & & \\ & & & & & \ddots & & \ddots & & \\ & & & & & & q & & p & \\ & & & & & & & q & & p \\ & & & & & & & & & 1 \end{bmatrix},\ q=1-p \end{gather*}

解得的列向量E\mathbf{E}中的每一个元素代表从某个胜负场状态开始到达升段/降段的期望局数。

当然，也可以把上述矩阵形式的线性方程组写成大家更熟悉的形式：

{Ei=(1−p)Ei−1+pEi+1+1,i∈{0,1,⋯ ,N−1}Ei=(1−p)Ei−1+pE1+1,i∈{−1,⋯ ,−M+1}EN=E−M=0\begin{dcases} E_i=(1-p)E_{i-1}+pE_{i+1}+1 &,i\in \{0,1,\cdots,N-1\}\\ E_i=(1-p)E_{i-1}+pE_1+1 &,i \in \{-1, \cdots, -M+1\}\\ E_N=E_{-M}=0 \end{dcases}

如果我们只关心E0E_0，那么和上一节类似，可以直接化简上面的线性方程组：

{E1=N−12p−1+(E0−N2p−1)pN(1−p)−p(1−p)NpN+1−p(1−p)NE0=(E1+1p)[1−(1−p)M]\begin{dcases} E_1=\dfrac{N-1}{2p-1}+\left(E_0-\dfrac{N}{2p-1}\right)\dfrac{p^N(1-p)-p(1-p)^N}{p^{N+1}-p(1-p)^N}\\ E_0=\left(E_1+\dfrac{1}{p}\right)\left[1-(1-p)^M\right] \end{dcases}

Last updated:

MIT Licensed | Copyright © 2021-2023 Lost Pieces - Locietta's Blog
Powered by VitePress